Why aren't there infinitely countable sigma-algebras?
This is a supplement to one of my analysis discussion sessions.
We will now prove a fascinating result in measure theory: there are no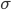 
-algebras that are infinitely countable. This means that any 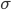-algebra 
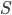is either finite (and is therefore just an algebra) or very 'BIG' in cardinality, in the sense that it is uncountable. The idea behind this proof is simple. We will take a 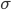-algebra 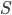on a set 
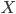, and show that the collection of `smallest' non-trivial sets belonging to 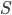are in one-to-one correspondence with a power set of a certain infinite set.
Let's assume by contradiction that 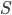is an infinitely countable 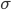-algebra defined on a set 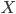. The set 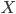has to be infinite as well (otherwise any 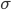-algebra defined on it is smaller in cardinality than its power set that is finite as well.) Define a function
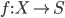
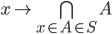
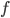maps 
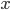to the smallest set of the 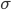-algebra 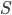that contains 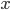. Note that this function is well-defined (and maps into 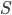) exactly because of the assumption that 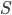is countable (and therefore any countable intersection remains in 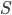by the definition of a 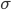-algebra.) Since 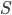is a collection of sets, the image of 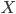under 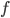is a subset of the power set of 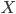. In fact, it turns out that 
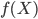provides us with a partition of .
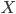Let's try to see why. Consider the images of two points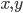 
under 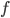and assume by contradiction they have a non-trivial intersection 
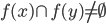. If 
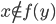then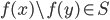 
is a smaller set in the 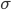-algebra containing 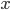which is a contradiction to the definition of 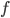. Therefore 
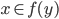and by the same argument 
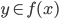. But then since 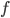maps a point to the smallest set in the 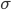-algebra containing it, 
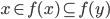and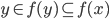 
and thus we conclude that 
.
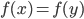We may conclude that 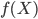is a partition of 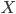. Each set 
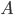in 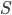can be written as the union of such images,
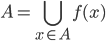
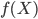cannot be finite, as otherwise 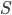would be finite as well. But now if the partition 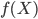is infinite, one can form all the sets in 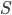by taking all the possible (disjoint) unions of sets in 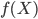. This means that the cardinality of 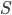is equal to the cardinality of the power set of 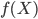, namely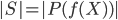 
This is a contradiction, and therefore the 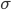-algebra 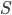cannot be infinitely countable.
Wow! This blog looks just like my old one! It's on a entirely different subject but it has pretty much the same page layout and design. Wonderful choice of colors!
Very nice proof!
Thanks!
I have one question. How do you know that for any A in S, you can write A as a countable union of f(x). You have A equals the union over all x in A of the sets f(x), but wouldn't you then be assuming that this is a countable union, i.e. A is a countable set?
Hey there. We don't assume it. We assumed $A$ is any union of $f(x)$, not necessarily a countable union...
Hi,if sometimes f(x)=f(y),you can not make sure you get enough disjoint sets to get the conclusion.How to fix it.I mean,take an extreme example,infinite f(x) is identical you just get finite f(x) is diffirent altough x is infinite.
I am sorry.I got it.We just need to prove f(x) is infinite
You don't need it here, but you *did* in fact already assume that the collection of A in S is countable in order to construct your set function, and thus arrive at the contradiction.
For me, the claim that S can be formed of all unions of the disjoint f(x) and this can be put into 1-1 correspondence with the power set of f(X) is where the rabbit goes into the hat. Is this simplyrics a well known fact from set theory? Because if it isn't the proof is incomplete.
It is straightforward if you consider the definition of f. Re-read "But now if the partition ...". Happy to elaborate if it's unclear.
i need some examples ...infinite sigma algebras ∈ N which is different form the Pot(N)
There are plenty online, e.g.:
http://math.stackexchange.com/questions/217275/give-an-example-of-sigma-algebra-in-mathcal-p-bbb-n
The last paragraph is problematic. You are saying that the map from $S \to P(f(X))$ given by
$A \mapsto \bigcup_{x \in A} f(x)$ is injective to argue that $f(X)$ should be infinite.
But then this would already imply that $|S| \geq |P(f(X))|$.
It's clear that $f(X)$ is infinite though (it is a partition of $X$). Hence the injectivity of this map clinges the deal.
Sorry but I haven't looked at this proof for a while. Where did I say it is injective? The only claim here is that its image is a partition...
I have one question .
Is the union of uncountably many sigma-fields also a sigma-fields?
Not necessarily...
oops...
then do you have any idea of counter example?
Well it is actually trickier than that. The union of sigma algebras is not necessarily a sigma algebra. However, you can look at the smallest sigma algebra that contains the union (and then you are guaranteed to get a sigma algebra...)
In this case there are plenty of example. A trivial one would be to define a sigma algebra S_x to be the smallest sigma algebra containing the singleton {x} (x = some real number). Then the smallest sigma algebra containing the union of S_x over all x in the real line would give you the power set of the real line.
Very nice example. Thanks
I understood your proof but I have a question that what is the need of showing that $f(X)$ partitions $S$,we could have argued by showing that the set of all distinct $f(x)$ is infinite without showing that $f(x)\cap \f(y)=\phi$ or $f(x)=f(y)$.
Sorry for not replying earlier. The partition approach is used in the sentence "But now if the partition..." - to show that the two cardinalities are equal.
There may be another way of doing it as you suggested...
Good job! Can you also show an example that a field can be countably infinite?
Q is an example of such field (the rationals).
I assumed you mean a field as in this definition (http://www.wikiwand.com/en/Field_(mathematics)) and not a sigma-field.