In physics, nearly every fundamental theory is based on a single underlying principle. For example, Lagrangian and Hamiltonian mechanics are based on the principle of least action, which states that the path taken by a physical system is the one for which the action is stationary. Similarly, the general theory of relativity is based on Einstein's principle of equivalence. The cornerstone of special relativity is the principle of relativity.

I always wanted to have my own principle. The main reason for this is that it would just be cool to use my principle in different occasions. Since I'm still not ready to publish any principles in theoretical physics, this might be a good opportunity to invent a principle for other aspects of life. I shall call it `the principle for serendipity' =). The principle of serendipity states that if you are thinking about something long (and strong) enough, you will have at least one remarkable serendipity related to what you were thinking about. This sounds silly, and it is supposed to be silly. But if you think about it, the more you think of something the more likely you are to notice events that are related to it (this is, among other reasons, why Sam Harris will never find a toast with Jesus' face, while some people do...)

So how is the principle of serendipity relates to the problem of self force? Well, I spent a big chunk of my week thinking about acceleration, self force and , where today I got a phone call from an old friend. My anonymous friend and myself studied together at the Technion, and after more than six years not seeing or talking to each other, he randomly called me explaining that he started thinking about radiation-reaction! Our conversation was the trigger for this post.

I've already discussed the problem of radiation reaction. The problem of radiation reaction is actually a special case of the self force problem (this connection will be discussed in a future post). Unlike the problem which has a pretty clear physical origin, the self force problem is fundamentally mathematical. Today, I'd like to discuss the mathematical origin of the self force problem.

In classical electrodynamics there are three kinds of problems we typically try to solve. The first problem is determining the motion of a charged particle in a known external field 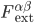. This amounts to solving the Lorentz force equation:
\begin{equation} \label{eq:LorentzForceExternal}
m \dot{u}^\alpha = -e F^{\alpha\beta} _{\text{ext}} u_\beta
\end{equation}
where 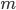is the mass of the particle, 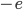is its charge, 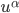is the four-velocity of the particle and the dot denotes a derivative with respect to proper time 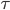. The Lorentz Force Eq. (\ref{eq:LorentzForceExternal}) is a second order ordinary differential equation for the four-position of the particle 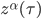. This means that the Lorentz Force Eq. (\ref{eq:LorentzForceExternal}) determines the worldline of the particle.

The Lorentz Force Eq. (\ref{eq:LorentzForceExternal}) may be linear or nonlinear in 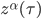, depending on the field supplied. However, whether linear or nonlinear, it is always a well-posed equation. This means that the Lorentz Force Eq. (\ref{eq:LorentzForceExternal}) admits a unique solution for the motion of the particle for any specified initial conditions 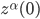and 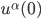and any specified external field 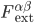(in fact, the external field need not be a solution of Maxwell's equations).

The second kind of problem is to determine the evolution of the field 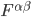for known charges / currents. In this case, one needs to solve Maxwell's equations
\begin{equation} \label{eq:Maxwell}
\partial_\alpha F^{\alpha\beta} = 4\pi J^\beta
\end{equation}
for a known four-current 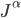. Eq. (\ref{eq:Maxwell}) is a system of first order linear partial differential equations, and their solution determines the evolution of the field 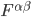. If you recall the other homogeneous Maxwell's equation, you will see that Maxwell's equations have a well posed initial value formulation, provided that the four-current 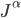is conserved, namely,
\begin{equation} \label{eq:CurrentConservation}
\partial_\alpha J^\alpha = 0
\end{equation}
Since Maxwell's equation (\ref{eq:Maxwell}) is linear, it makes a perfect mathematical sense to let 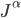be a distribution (e.g. the almighty Dirac delta function), in which case the corresponding field solution 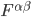will be a distribution as well. For example, even for a point particle source of the form
\begin{equation} \label{eq:FourCurrent}
J^\alpha = -e u^\alpha \delta ^{(3)} (x^i - z^i (t)) \frac{d\tau}{dt}
\end{equation}
the Maxwell Eq. (\ref{eq:Maxwell}) is well-defined, provided that the worldline is timelike and that is constant along it.

So far so good. Now for the fun part.

Since the Lorentz force Eq. (\ref{eq:LorentzForceExternal}) is well-posed for a point particle in any external field, and Maxwell's Eq. (\ref{eq:Maxwell}) is well-posed for any point particle source, one might expect the coupled system to be well-posed as well. In other words, one might expect that the coupled problem 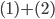will be self-consistent also if you replace the external field 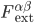in Eq. (\ref{eq:LorentzForce}) with the full electromagnetic field ,
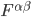\begin{equation} \label{eq:LorentzForce}
m \dot{u}^\alpha = -e F^{\alpha\beta} u_\beta
\end{equation}

However, it is easy to see that this is not the case, as the full electromagnetic field 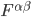is necessarily singular along the worldline of the particle. Consequently, Eq. (\ref{eq:LorentzForce}) is necessarily ill-defined. Therefore, the coupled system of equations (\ref{eq:Maxwell}), (\ref{eq:FourCurrent}) and (\ref{eq:LorentzForce}) doesn't make any mathematical sense.

This is the self force problem . The fact that the full electromagnetic field 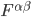now contains the "self-field" of the point charge, makes it ill-defined along the particle itself. We see that the problem is mathematical in origin. It should be clear now that the self force problem is a result of us treating the particle as a point particle and using distribution theory.

People tried to solve the self force problem in different ways. Lorentz and Poincaré attempted on giving the electron a structure so it is not a point particle anymore. In this case a new problem arises, which is the question of what forces are holding the electron together (together with the fact that current experiment still haven't observed any signs of a non-trivial structure for the electron). Other physicists, including Dirac (1938) and Gralla et al. (2009) decided to take a more practical point of view, and considered the particle as a point particle as reached from a structured particle using a well-defined limit. This approach requires renormalization procedures or rather hardcore perturbation theory.

Interestingly, many scientists believe this self force problem is a not really a problem. They think the problem is a result of us using classical electrodynamics, and that the problem disappears once the situation is analyzed in quantum electrodynamics. I'll remind those folks that in quantum field theory we still use delta functions and renormalization theory. Do you think the legendary Paul Dirac would have spent his time in 1938 working on a problem that he apparently solved ten years beforehand with quantum mechanics?

More to come.