Electromagnetic field lines are as old as electromagnetic theory itself. Practically every physics student learns about field lines as a way to imagine and visualize the electric and magnetic fields. Field lines are useful pedagogical tools, but can they be more than that?

Michael Faraday, who developed the concept of field lines, referred to them as 'lines of force'. Faraday thought of reality as being made out of the force itself. For Faraday field lines were real physical entities, and not merely pedagogical tools.

In this series of posts I'll demonstrate a very profound relationship I co-discovered between electromagnetic field lines and acceleration of charges.

We will begin with a well known result of special relativity. The field lines created by a charge at rest are isotropic. In fact, such field lines are not only identical in all directions, they also are straight (a fact that will be important in what follows). If the same charge is traveling with a constant velocity relatively to our laboratory, then special relativity teaches us that the field lines remain straight, but now they are denser in the direction perpendicular to the motion of the charge.

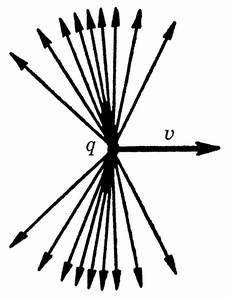
The electric field lines of a uniformly moving charge are denser in the direction perpendicular to the direction of motion.

When we start with a resting charge and instantaneously change its velocity, it emits an electromagnetic wave. For a sufficiently far observer the charge still appears to be at rest, and its field-line appear isotropic outside of the light-cone. Inside the light-cone, the charge is already moving, hence the field-lines appear denser in the direction perpendicular to the direction of motion.

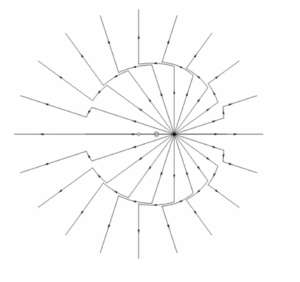
When a resting charge abruptly starts moving, an electromagnetic wave is formed. The field lines are isotropic outside of the light cone. Inside the light cone the field lines are denser in the direction perpendicular to the direction of motion.

So far, everything I wrote should be familiar to any student who took a basic electromagnetism class. This really starts to gets exciting once you start considering accelerating charges.

Consider a uniformly accelerating charge. The previous figure hints on what will happen in this case, and it is an easy exercise to show that now the electric field lines curve nearby the charge:

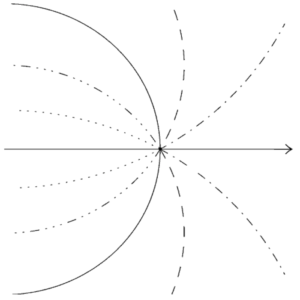
Electric field lines of a uniformly accelerating charge are curved. The charge accelerates in the direction of flat field lines.

The acceleration of the charge bends the field lines around the charge. This picture reveals two things:

• The field lines near an accelerating charge bend.
• The charge accelerates in the direction of straight (flat) field lines.

In other words, acceleration of charges implies curvature of electric field lines. Implications are interesting, but equivalences between different concepts are stronger and reveal much more about the natural world. So the question my colleagues and I asked ourselves was whether there is something deeper in this statement. Do field lines curve nearby charges precisely when charges accelerate?

It turns out that the answer is yes. In this series of posts I'll prove the following results:

Electromagnetic field lines curve nearby a charge if and only if the charge accelerates. Moreover, charges always accelerate in the direction of straight (flat) field lines.

It turns out this beautifully generalizes to relativistic cases and to the full electromagnetic field, and there is even a connection to gravity that we will explore. Moreover, this relationship between field lines curvature and acceleration can be captured by a very simple action principle that resolves what is probably the oldest problem of all field theories.

Field Lines and Acceleration: Part II (Coming soon)