Continuity of the translation mapping in L^1
A problem from class. Fix an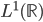 
function 
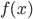. Define the translation mapping 
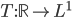sending 
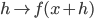. How does one prove that 
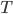is continuous at 
?
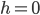We begin by proving it for a dense set. One can either use compactly supported continuous functions, or instead 'very simple functions' (my own terminology). Let us use the latter, but I recommend you to try and prove it using compactly supported continuous function as well. By a 'very simple function', I mean a simple function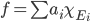 
where the 'very' means that each 
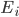is an open interval. Given such a function 
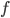, we notice that by the triangle inequality,
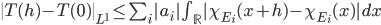
However, it's not hard to see that this integral (for a fixed
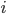) is the measure of the symmetric difference of 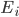and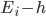 
. One can easily compute this integral, and show that this symmetric difference is either twice the measure of 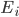(whenever 
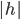is larger than the measure of 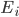) or is 2|h| (when 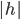is smaller than the measure of 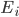). Note that this calculations hold because we assumed 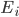to be an open interval. Thus, if 
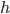is small enough (small enough means smaller than the measure of all the 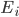's), we have
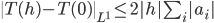
and therefore
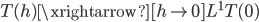
This proves the statement for 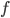being a 'very simple function'. Let us now prove it in the general case. Let 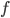be any 
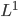function. Fix 
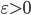and take a 'very simple function' 
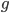such that 
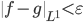. By the triangle inequality,
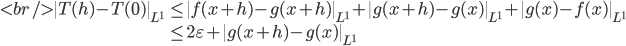
where the last line holds because of the translation invariance of the Lebesgue integral. Now since 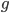is a 'very simple function' for which we already proven the translation to be continuous, when taking the limit 
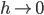we get
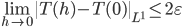
This is of course true for all 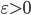, and therefore
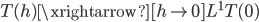
Recent Comments